De wet van Zipf eindelijk verklaard?
Een stukje op de site van Onze Taal intrigeerde me. De titel van het stuk: Verklaring gevonden voor honderd jaar oude taalkundige wet. Ik had nog nooit van deze wet gehoord. Maar ik ben dan ook geen taalkundige, maar een letterkundige. In het kort gaat de wet van Zipf over ‘hoe de frequentie van een woord in natuurlijke taal afhankelijk is van zijn rangorde in een frequentietelling’. Geen zorgen, ik begreep het ook niet. Reden om op onderzoek te gaan dus.
De wet van Zipf is vernoemd naar zijn ontdekker: George Kingsley Zipf (1902-1950), een Amerikaanse taalkundige. Hij zei, dat het meestvoorkomende woord in een natuurlijke taal twee keer zo vaak voorkomt als het woord dat het op een na meestvoorkomende woord is en drie keer zoveel als het twee na meestvoorkomende woord en zo verder tot het minst voorkomende woord in een natuurlijke taal. Voor deze wet is nu een verklaring gevonden door taalwetenschapper Sander Lestrade.
Wat is een natuurlijke taal?
Een natuurlijke taal is een taal die door een aantal sprekers als moedertaal gezien wordt, of deze taal nu dood of levend is. Het Latijn en het Nederlands zijn allebei natuurlijke talen, ook al is Latijn een dode taal. De talen werden en worden van generatie op generatie doorgegeven.
De wet van Zipf verder uitgelegd
Deze wet markeert het begin van de computationele taalkunde. Computationele taalkunde wil, kort door de bocht, zeggen dat men gaat rekenen met taal. Er worden onderzoek gedaan naar taal in verschillende onderdelen daarvan, bijvoorbeeld syntaxis, semantiek, fonetiek, fonologie en sociolinguïstiek. De resultaten van onderzoek zijn vaak modellen waarin taalkundige verschijnselen worden uitgelegd met een berekening. De spellingschecker van Word is een voorbeeld van computationele linguïstiek, deze ‘berekent’ (corrigeert en detecteert) namelijk spelfouten.
Zipf bestudeerde in 1930 het werk Ulysses van James Joyce. Het viel hem op dat het woord the twee keer vaker voorkwam dan het woord of en drie keer vaker dan het woord dat daarna het meestgebruikte Engelse woord is. Het bleek ook dat dit niet alleen voor het Engels opging, maar ook voor andere talen. Zo kwam hij erachter dat de mogelijkheid bestond om een frequentietabel op te stellen voor het woordgebruik, de zogenaamde Zipf-distributie of Zipf-curve. De Zipf-curve is een exponentieel dalende lijn.:
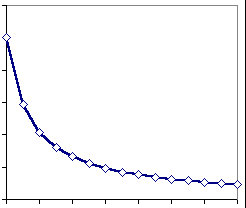
Zipf-curve of Zip-fdistributie
Er was echter nog nooit een verklaring gevonden voor de wet van Zipf
Tot nu. Sander Lestrade van de Radboud Universiteit in Nijmegen heeft een taalkundige onderbouwing gevonden voor de wet van Zipf. Ik zet het woordje een hier schuin, omdat er natuurlijk altijd nog andere oplossingen mogelijk zijn. Lestrade heeft zijn oplossing gepubliceerd in het taalkundig tijdschrift PLOS One en op de website van de Universiteit.
Zijn oplossing is gebaseerd op het feit dat syntaxis (de leer van de zinsbouw) en semantiek (de leer van woord en betekenis) elkaar nodig hebben om die verdeling tot stand te brengen. Dat zit zo. Het Nederlands heeft drie lidwoorden: de, het en een. We hebben echter tienduizenden zelfstandige naamwoorden. Die lidwoorden staan over het algemeen bijna altijd voor een zelfstandig naamwoord. Het is dus redelijk logisch, dat lidwoorden vaker voorkomen dan zelfstandige naamwoorden.
Lestrade zegt, dat dit echter niet voldoende is om de wet te verklaren. Die tienduizenden zelfstandige naamwoorden hebben verschillende klassen: het woord ding komt vaker voor dan onderzeeboot. Ding gebruik je dus vaker dan onderzeeboot. Het gaat in die klassen dus om hoe specifiek een woord is. Een woord mag niet te specifiek zijn, maar ook niet te algemeen. Lestrade zegt dat je de betekenisverschillen van woorden binnen woordklassen moet ‘vermenigvuldigen’ met de behoefte aan die klasse.
Dat blijft wel een beetje abstract
Een woord als onderzeeboot is veel te specifiek. Tenzij je bij de marine zit, of die dingen bouwt, zul je het woord niet vaak gebruiken. Als een woord voor veel dingen gebruikt kan worden, dan wordt het ambigu. Alleen woorden kunnen dus de wet van Zipf niet verklaren. Het combineren van woorden in zinnen, levert wel de Zipfiaanse curve op, inclusief de afwijking die in de natuurlijke taal te vinden is.
Als je meer in detail wil lezen hoe Lestrade dit heeft aangepakt, kijk dan bij de link naar PLOS One. Daar staat het volledige artikel in het Engels.
Ik merk dat dit een lastig onderwerp is. Ook voor mij. Maar ik vind het wel leuk om te beschrijven en bij te houden. Ik ga dit echt vaker doen, al is het alleen maar voor mijzelf, om het zelf te snappen.
Meer weten of vragen?
Ben je geïnteresseerd geraakt door dit blog? Stuur me een berichtje en help je verder!
Ik geloof ook niet dat ik het helemaal snap, ik zal het eens doorsturen naar een vriendin die Engels heeft gestudeerd en vast wel hiervan heeft gehoord.